高数基础知识(下)
本文最后更新于 2025-09-11 10:02:28
四、不定积分
4.1 基本概念
若 $F(x)$ 为 $f(x)$ 在某区间内的原函数,则 $F(x) + C$($C$ 为任意常数)也为 $f(x)$ 在该区间内的原函数。
若 $F(x), G(x)$ 都是 $f(x)$ 在某区间内的原函数,则 $F(x) - G(x) = C$($C$ 为某个确定常数)。
不定积分
定义 $f(x)$ 的原函数的全体称为 $f(x)$ 的不定积分,记为 $\int f(x) dx$。
如果 $F(x)$ 为 $f(x)$ 的一个原函数,则有
$$\int f(x) dx = F(x) + C, \text{ 其中 } C \text{ 为任意常数。}$$
不定积分的几何意义
设 $F(x)$ 为 $f(x)$ 的一个原函数,则从几何上看,$F(x)$ 表示平面上的一条曲线,称为 $f(x)$ 的积分曲线。因此,不定积分 $$\int f(x) dx = F(x) + C$$ 在几何上表示一簇积分曲线。这簇分曲线对应于横坐标 $x$ 处的切线都相互平行。
原函数存在定理
定理 若 $f(x)$ 在区间 $I$ 上连续,则 $f(x)$ 在区间 $I$ 上一定存在原函数。
定理 若 $f(x)$ 在区间 $I$ 上有第一类间断点,则 $f(x)$ 在区间 $I$ 上没有原函数。
4.2 不定积分性质和公式
(1)不定积分的性质
(1) $\left( \int f(x) dx \right)’ = f(x), \quad d \int f(x) dx = f(x) dx.$
(2) $\int f’(x) dx = f(x) + C, \quad \int df(x) = f(x) + C.$
(3) $\int [f(x) \pm g(x)] dx = \int f(x) dx \pm \int g(x) dx.$
(4) $\int kf(x) dx = k \int f(x) dx \quad (k \text{ 为常数}).$
(2)不定积分基本公式
(1) $\int 0 dx = C.$
(2) $\int x^a dx = \frac{1}{a+1} x^{a+1} + C \quad (a \neq -1).$
(3) $\int \frac{1}{x} dx = \ln |x| + C.$
(4) $\int a^x dx = \frac{a^x}{\ln a} + C \quad (a > 0, a \neq 1).$
(5) $\int e^x dx = e^x + C.$
(6) $\int \sin x dx = -\cos x + C.$
(7) $\int \cos x dx = \sin x + C.$
(8) $\int \sec^2 x dx = \tan x + C.$
(9) $\int \csc^2 x dx = -\cot x + C.$
(10) $\int \sec x \tan x dx = \sec x + C.$
(11) $\int \csc x \cot x dx = -\csc x + C.$
(12) $\int \frac{1}{\sqrt{1-x^2}} dx = \arcsin x + C.$
(13) $\int \frac{1}{1+x^2} dx = \arctan x + C.$
(14) $\int \frac{dx}{\sqrt{a^2-x^2}} = \arcsin \frac{x}{a} + C.$
(15) $\int \frac{dx}{a^2+x^2} = \frac{1}{a} \arctan \frac{x}{a} + C.$
(16) $\int \frac{dx}{x^2-a^2} = \frac{1}{2a} \ln \left| \frac{x-a}{x+a} \right| + C.$
(17) $\int \frac{dx}{\sqrt{x^2+a^2}} = \ln(x+\sqrt{x^2+a^2}) + C$
(18) $\int \frac{dx}{\sqrt{x^2-a^2}} = \ln |x+\sqrt{x^2-a^2}| + C$
(19) $\int \sec x dx = \ln |\sec x + \tan x| + C$
(20) $\int \csc x dx = -\ln |\csc x + \cot x| + C$
4.3 三种主要积分法
4.3.1 第一换元积分法
定理 设 $$\int f(u) du = F(u) + C, \quad u = \varphi(x)$$ 存在连续导数,则
$$\int [f(\varphi(x))] \varphi’(x) dx = \int f[\varphi(x)] d\varphi(x) = F[\varphi(x)] + C.$$
常见的凑微分形式:
(1) $\int f(ax + b) dx = \frac{1}{a} \int f(ax + b) d(ax + b)$
(2) $\int x^m f(ax^{m+1} + b) dx = \frac{1}{(m+1)a} \int f(ax^{m+1} + b) d(ax^{m+1} + b) \quad (m \ne -1)$
(3) $\int f(\sqrt{x}) \frac{dx}{\sqrt{x}} = 2 \int f(\sqrt{x}) d(\sqrt{x})$
(4) $\int f(e^x) e^x dx = \int f(e^x) d(e^x)$
(5) $\int f(\ln x) \frac{1}{x} dx = \int f(\ln x) d(\ln x)$
(6) $\int f(\sin x) \cos x dx = \int f(\sin x) d(\sin x)$
(7) $\int f(\cos x) \sin x dx = -\int f(\cos x) d(\cos x)$
(8) $\int f(\tan x) \frac{1}{\cos^2 x} dx = \int f(\tan x) d(\tan x)$
(9) $\int f(\arcsin x) \frac{1}{\sqrt{1-x^2}} dx = \int f(\arcsin x) d(\arcsin x)$
(10) $\int f(\arctan x) \frac{1}{1+x^2} dx = \int f(\arctan x) d(\arctan x)$
求不定积分 $\int \sec^4 x dx$,
解 (1) $\int \sec^4 x dx = \int \sec^2 x d(\tan x) = \int (\tan^2 x + 1) d(\tan x)$
$= \frac{1}{3} \tan^3 x + \tan x + C$
4.3.2 第二换元积分法
定理 设 $x = \varphi(t)$ 是单调的、可导的函数,并且 $\varphi’(t) \neq 0$。又
$$\int f[\varphi(t)]\varphi’(t)dt = F(t) + C$$则
$$
\begin{align*}
\int f(x)dx &= \int f[\varphi(t)]\varphi’(t)dt \\&= F(t) + C\\
&= F[\varphi^{-1}(x)] + C
\end{align*}
$$
其中 $\varphi^{-1}(x)$ 是 $x = \varphi(t)$ 的反函数。
常用的三种变量代换:
(1) 被积函数含有 $\sqrt{a^2 - x^2}$,令 $x = a \sin t$(或 $a \cos t$)
(2) 被积函数含有 $\sqrt{a^2 + x^2}$,令 $x = a \tan t$
(3) 被积函数含有 $\sqrt{x^2 - a^2}$,令 $x = a \sec t$
4.3.3 分部积分法
(1) 分部积分法所适用的函数类
$$
\int u d v=uv-\int v d u
$$
(2) 分部积分法所适用的函数类
分部积分法比较适用于两类不同函数相乘。如下列积分,这里 $ p_n(x) $ 为 $ x $ 的 $ n $ 次多项式。
$$
\int p_n(x) e^{ax} dx, \quad \int p_n(x) \sin ax dx,\int p_n(x) \cos ax dx,\quad \int e^{ax} \sin ax dx,
$$
$$
\int e^{ax} \cos ax dx, \quad \int p_n(x) \ln x dx,\int p_n(x) \arctan x dx, \quad \int p_n(x) \arcsin x dx.
$$
(3) 分部积分法中 ( u,v ) 的选取
分部积分法在使用时的关键是 ( u,v ) 的选取,换句话说就是把哪个数凑到微分号里去。
- $\int p_n(x) e^{ax} dx, \int p_n(x) \sin ax dx, \int p_n(x) \cos ax dx$,这3种积分都应多项式以外的函数凑进微分号。
- $\int e^{ax} \sin ax dx, \int e^{ax} \cos ax dx$,这2种积分把指数函数或三角函数凑进微分号都可以,但把指数凑进去更简单,连续两次将指数函数凑进去分部积分还原便可求解。
- $\int p_n(x) \ln x dx, \int p_n(x) \arctan x dx, \int p_n(x) \arcsin x dx$,这3种积分都应多项式函数凑进微分号。
4.3.4 常见可积函数积分
4.3.4.1 三角有理式积分
$$
\int R(\sin x, \cos x) dx
$$
(1) 一般方法(万能代换)
令 $\tan \frac{x}{2} = t$,
$$
\int R(\sin x, \cos x) dx = \int R\left( \frac{2t}{1+t^2}, \frac{1-t^2}{1+t^2} \right) \frac{2}{1+t^2} dt
$$
(2) 特殊方法(三角变形,换元,分部)
几种常用的换元法:
若 $R(-\sin x, \cos x) = -R(\sin x, \cos x)$,则令 $u = \cos x$,或凑 $d \cos x$。
若 $R(\sin x, -\cos x) = -R(\sin x, \cos x)$,则令 $u = \sin x$,或凑 $d \sin x$。
若 $R(-\sin x, -\cos x) = R(\sin x, \cos x)$,则令 $u = \tan x$,或凑 $d \tan x$。
4.3.4.2 有理函数积分
(1)一般方法(部分分式法)
(2)特殊方法(加减拆项或凑微分降幂)
对可积函数积分 $\int \frac{A x + b y x}{(x - 1)^p (x^2 + x + 1)^q} dx$
有
$\frac{A}{x - 1} + \frac{B}{(x - 1)^2} + \cdots + \frac{B}{ (x - 1)^p} + \frac{C_1 x + D_1}{x^2 + x + 1} + ··· +\frac{C_2 x + D_2}{(x^2 + x + 1)^q}$
- 其中 $A x + b$ 只是一种形式,对拆分无影响。
- 分母中自变量系数与常量对拆分无影响。
学基础篇
【例12】(2019,数二)求不定积分 $\int \frac{3x+6}{(x-1)^2(x^2+x+1)} dx$
令 $\frac{3x+6}{(x-1)^2(x^2+x+1)} = \frac{A}{x-1} + \frac{B}{(x-1)^2} + \frac{Dx+E}{x^2+x+1}$,则
$3x+6 = A(x-1)(x^2+x+1) + B(x^2+x+1) + (Dx+E)(x-1)^2$
所以
$$
\begin{cases}
A + D = 0\\
B - 2D + E = 0\\
B + D - 2E = 3 \\
-A + B + E = 6
\end{cases}
$$
解得
$$
\begin{cases}
A = -2 \\
B = 3\\
D = 2 \\
E = 1
\end{cases}
$$
则
$$
\begin{align*}
\int \frac{3x+6}{(x-1)^2(x^2+x+1)} dx &= \int \frac{-2}{x-1} dx + \int \frac{3}{(x-1)^2} dx + \int \frac{2x+1}{x^2+x+1} dx\\
&= -2 \ln |x-1| - \frac{3}{x-1} + \ln (x^2+x+1) + C
\end{align*}
$$
4.3.4.3 无理函数积分
简单无理函数积分 $\int R\left( x, \sqrt{\frac{ax+b}{cx+d}} \right) dx$
令 $\sqrt{\frac{ax+b}{cx+d}}=t$,将其化为有理函数积分进行计算。
计算 $\int \frac{1}{x} \sqrt{\frac{x+1}{x}} dx$。
解 【方法1】
令 $\sqrt{\frac{x+1}{x}}=t$,则 $x=\frac{1}{t^2-1}$,$dx=-\frac{2t}{(t^2-1)^2} dt$,
$\int \frac{1}{x} \sqrt{\frac{x+1}{x}} dx $
$= \int (t^2-1) t \frac{-2t}{(t^2-1)^2} dt$
$ = -2 \int \left( 1+\frac{1}{t^2-1} \right) dt$
$= -2 \left( t + \frac{1}{2} \ln \left| \frac{t-1}{t+1} \right| \right) + C$
$= -2 \sqrt{1+\frac{1}{x}} - \ln \left| 2x + 1 - 2x \sqrt{1+\frac{1}{x}} \right| + C$
【方法2】分子有理化。
$\int \frac{1}{x} \sqrt{\frac{x+1}{x}} dx$
$ = \int \frac{x+1}{x \sqrt{x^2+x}} dx$
$= \int \frac{d \left( x + \frac{1}{2} \right)}{\sqrt{\left( x + \frac{1}{2} \right)^2 - \frac{1}{4}}} + \int \frac{dx}{x^2 \sqrt{1+\frac{1}{x}}}$
$= \ln \left| x + \frac{1}{2} + \sqrt{\left( x + \frac{1}{2} \right)^2 - \frac{1}{4}} \right| - \int \frac{d \left( 1 + \frac{1}{x} \right)}{\sqrt{1+\frac{1}{x}}}$
$= \ln \left| x + \frac{1}{2} + \sqrt{x^2 + x} \right| - 2 \sqrt{1 + \frac{1}{x}} + C$
五、定积分
5.1 定积分的几何意义
(1) 设 $\int_a^b f(x) dx$ 存在,若在 $[a,b]$ 上 $f(x) \geq 0$,则 $\int_a^b f(x) dx$ 的值等于以曲线 $y = f(x)$、$x = a$、$x = b$ 及 $x$ 轴所围成的曲边梯形的面积。
(2) 若在 $[a,b]$ 上 $f(x) \leq 0$,则 $\int_a^b f(x) dx$ 的值等于以曲线 $y = f(x)$、$x = a$、$x = b$ 及 $x$ 轴所围成的曲边梯形面积的负值。
(3) 若在 $[a,b]$ 上 $f(x)$ 的值有正也有负,则 $\int_a^b f(x) dx$ 的值等于 $x$ 轴上方的面积减去 $x$ 轴下方的面积所得之差。
5.2 定积分的性质
1. 不等式性质
(1) 若在区间 $[a,b]$ 上 $f(x) \leq g(x)$,则 $\int_{a}^{b} f(x) dx \leq \int_{a}^{b} g(x) dx$
(2) 若 $M$ 及 $m$ 分别是 $f(x)$ 在 $[a,b]$ 上的最大值和最小值,则 $$m(b-a) \leq \int_{a}^{b} f(x) dx \leq M(b-a)$$
(3) $\left| \int_{a}^{b} f(x) dx \right| \leq \int_{a}^{b} |f(x)| dx$
2. 中值定理
(1) 若 $f(x)$ 在 $[a,b]$ 上连续,则
$$\int_{a}^{b} f(x) dx = f(\xi)(b-a) \quad (a < \xi < b)$$
常称 $\frac{1}{b-a} \int_{a}^{b} f(x) dx$ 为函数 $y = f(x)$ 在区间 $[a,b]$ 上的平均值
(2) 若 $f(x), g(x)$ 在 $[a,b]$ 上连续,$g(x)$ 不变号,则
$$\int_{a}^{b} f(x) g(x) dx = f(\xi) \int_{a}^{b} g(x) dx \quad (a \leq \xi \leq b)$$
定理 设$f(x)$在 $[-L,L]$ 上连续,则
如果$f(x)$为奇函数,那么 $\int_{0}^{x} f(t) dt$为偶函数
如果 $f(x)$ 为偶函数,那么 $\int_{0}^{x} f(t) dt$ 必为奇函数。
5.3 积分上限的函数
变上限的积分 $\int_{a}^{x} f(t) dt$ 是其上限 $x$ 的函数,常称之为积分上限函数。
定理 如果 $f(x)$ 在区间 $[a,b]$ 上连续,则 $\Phi(x) = \int_{a}^{x} f(t) dt$ 在 $[a,b]$ 上可导,且 $\frac{d\Phi(x)}{dx} = f(x)$
由原函数的概念可知,如果 $f(x)$ 在区间 $[a,b]$ 上连续,则 $\Phi(x) = \int_{a}^{x} f(t) dt$ 为 $f(x)$ 在区间 $[a,b]$ 上的一个原函数。由此可知,连续函数必有原函数。
【注】 如果 $f(x)$ 为 $[a,b]$ 上的连续函数,$\varphi_1(x), \varphi_2(x)$ 为可导函数,则 (积分求导)
$$\left( \int_{\varphi_1(x)}^{\varphi_2(x)} f(t) dt \right)’ = f[\varphi_2(x)] \cdot \varphi_2’(x) - f[\varphi_1(x)] \cdot \varphi_1’(x)$$
二重积分求导:
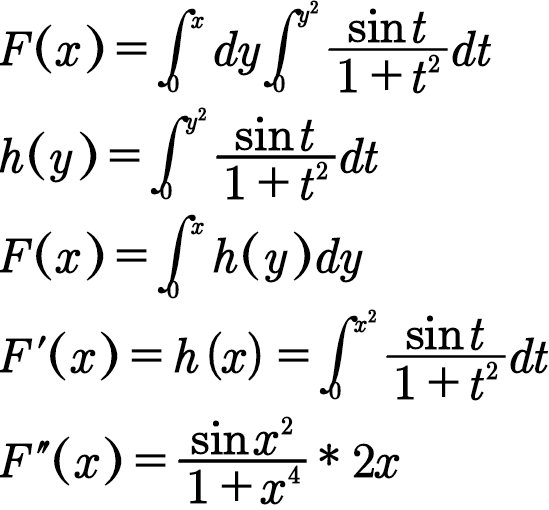
5.4 定积分的积分方法
定积分的计算主要有以下五种方法:
5.4.1 牛顿—莱布尼茨公式
设 $f(x)$ 在区间 $[a,b]$ 上连续,$F(x)$ 为 $f(x)$ 在 $[a,b]$ 上的一个原函数,则有
$$
\int_a^b f(x) dx = F(x) \bigg|_a^b = F(b) - F(a)。
$$
5.4.2 换元积分法
设 $f(x)$ 在区间 $I$ 上连续,函数 $x = \varphi(t)$ 满足以下条件:
- $\varphi(\alpha) = a, \varphi(\beta) = b$。
- $\varphi(t)$ 在 $[\alpha,\beta]$(或 $[\beta,a]$)上有连续导数,且 $R_\varphi \subseteq I$,则
$$
\int_a^b f(x) dx = \int_\alpha^\beta f[\varphi(t)] \varphi’(t) dt。
$$
5.4.3 分部积分法
$$
\int_a^b u dv = uv \bigg|_a^b - \int_a^b v du。
$$
5.4.4 利用奇偶性和周期性
(1) 设 $f(x)$ 为 $[-a,a]$ 上的连续函数 ($a>0$),则
$$
\int_{-a}^{a} f(x) dx =
\begin{cases}
0, & f(x) \text{为奇函数时}, \\
2 \int_{0}^{a} f(x) dx, & f(x) \text{为偶函数时}.
\end{cases}
$$
(2) 设 $f(x)$ 是以 $T$ 为周期的连续函数,则对任给数 $a$,总有
$$
\int_{a}^{a+T} f(x) dx = \int_{0}^{T} f(x) dx.
$$
5.4.5 利用已有公式
(1)
$$
\int_{0}^{\frac{\pi}{2}} \sin^n x dx = \int_{0}^{\frac{\pi}{2}} \cos^n x dx =
\begin{cases}
\frac{n-1}{n} \cdot \frac{n-3}{n-2} \cdots \frac{1}{2} \cdot \frac{\pi}{2}, & n \text{为正偶数}\\
\frac{n-1}{n} \cdot \frac{n-3}{n-2} \cdots \frac{2}{3}, & n \text{为大于1的奇数}
\end{cases}
$$
(2)
$$
\int_{0}^{\pi} x f(\sin x) dx = \frac{\pi}{2} \int_{0}^{\pi} f(\sin x) dx \quad (\text{其中} f(x) \text{连续}).
$$
5.5 判断原函数的可导性

5.6 定积分的应用
平面图形的面积
(1) 若平面域 $D$ 由曲线 $y = f(x)$, $y = g(x)$ ($f(x) \geq g(x)$), $x = a$, $x = b$ ($a < b$) 所围成,则平面域 $D$ 的面积为 $S = \int_a^b [f(x) - g(x)] dx$
(2) 若平面域 $D$ 由曲线 $r = r(\theta)$, $\theta = \alpha$, $\theta = \beta$ ($\alpha < \beta$) 所围成,则其面积为 $S = \frac{1}{2} \int_{\alpha}^{\beta} r^2 (\theta) d\theta$
旋转体体积
若区域 $D$ 由曲线 $y = f(x)$ ($f(x) \geq 0$) 和直线 $x = a$, $x = b$ ($0 \leq a < b$) 及 $x$ 轴所围成,则
(1)区域 $D$ 绕 $x$ 轴旋转一周所得到的旋转体体积为
$$V_x = \pi \int_a^b f^2(x) dx$$
(2) 区域 $D$ 绕 $y$ 轴旋转一周所得到的旋转体体积为
$$V_y = 2\pi \int_a^b xf(x) dx$$
曲线弧长
(1) $C: y = y(x), a \leq x \leq b.$
$$s = \int_a^b \sqrt{1 + y’^2} dx$$
(2) $C: \begin{cases} x= x(t), \\ y= y(t), \end{cases} a\leq t \leq b.$
$$s = \int_a^b \sqrt{x’^2 + y’^2} dt$$
(3) $C: r = r(\theta), a \leq \theta \leq b$
$$s = \int_a^b \sqrt{r^2 + r’^2}dt$$
旋转体侧面积
曲线 $ y = f(x) (f(x) \geq 0) $ 和直线 $ x = a, x = b (0 \leq a < b) $及 $ $轴所围成区域绕 $x $ 轴旋转所得旋转体的侧面积为
$$S = 2\pi \int_{a}^{b} f(x) \sqrt{1 + f’^{2}(x)} \mathrm{d}x$$
六、反常积分
6.1 无穷区间上的反常积分
定义
(1) 设 $f(x)$ 为 $[a, +\infty)$ 上的连续函数,如果极限 $\lim\limits_{x \to +\infty} \int_a^x f(x) dx$ 存在,则称原函数 $f(x)$ 在无穷区间 $[a, +\infty)$ 上的反常积分,记作 $\int_a^{+\infty} f(x) dx$
$$\int_a^{+\infty} f(x) dx = \lim\limits_{x \to +\infty} \int_a^x f(x) dx$$
这时也称反常积分 $\int_a^{+\infty} f(x) dx$ 收敛。如果上述极限不存在,则称反常积分 $\int_a^{+\infty} f(x) dx$ 发散。
(2) 设 $f(x)$ 为 $(-\infty, b]$ 上的连续函数,则可类似的定义函数 $f(x)$ 在无穷区间 $(-\infty, b]$ 上的反常积分
$$\int_{-\infty}^b f(x) dx = \lim\limits_{x \to -\infty} \int_b^x f(x) dx$$
(3) 设 $f(x)$ 为 $(-\infty, +\infty)$ 上的连续函数,如果反常积分
$$\int_{-\infty}^0 f(x) dx$$ 和 $$\int_0^{+\infty} f(x) dx$$
都收敛,则称反常积分 $\int_{-\infty}^{+\infty} f(x) dx$ 收敛,且
$$\int_{-\infty}^{+\infty} f(x) dx = \int_{-\infty}^0 f(x) dx + \int_0^{+\infty} f(x) dx$$
如果 $\int_{-\infty}^0 f(x) dx$ 与 $\int_0^{+\infty} f(x) dx$ 至少有一个发散,则称 $\int_{-\infty}^{+\infty} f(x) dx$ 发散。
定理 1(比较判别法)
设 $f(x), g(x)$ 在 $[a, +\infty)$ 上连续,且 $0 \leq f(x) \leq g(x)$,则
(1) 当 $\int_a^{+\infty} g(x) dx$ 收敛时,$\int_a^{+\infty} f(x) dx$ 收敛。
(2) 当 $\int_a^{+\infty} f(x) dx$ 发散时,$\int_a^{+\infty} g(x) dx$ 发散。
定理 2(比较判别法的极限形式)
设 $f(x), g(x)$ 在 $[a, +\infty)$ 上非负连续,且 $\lim\limits_{x \to +\infty} \frac{f(x)}{g(x)} = \lambda$(有限或无穷),则
(1) 当 $\lambda \neq 0$ 时,$\int_a^{+\infty} f(x) dx$ 与 $\int_a^{+\infty} g(x) dx$ 同敛散。
(2) 当 $\lambda = 0$ 时,若 $\int_a^{+\infty} g(x) dx$ 收敛,则 $\int_a^{+\infty} f(x) dx$ 也收敛。
(3) 当 $\lambda = +\infty$ 时,若 $\int_{a}^{+\infty} g(x) dx$ 发散,则 $\int_{a}^{+\infty} f(x) dx$ 也发散。
常用结论:
$$
\int_{a}^{+\infty} \frac{1}{x^p} dx
\begin{cases}
p > 1,收敛\\ p \leq 1$,发散
\end{cases}
\quad (a > 0)
$$
6.2 无界函数的反常积分
如果函数 $f(x)$ 在点 $a$ 的任一邻域内都无界,那么点 $a$ 称为函数 $f(x)$ 的瑕点(也称为无界点)。无界函数的反常积分也称为瑕积分。
定义
(1) 设函数 $f(x)$ 在 $[a,b]$ 上连续,点 $a$ 为函数 $f(x)$ 的瑕点。如果极限
$$\lim\limits_{t \to a^+} \int_t^b f(x) dx$$
存在,则称此极限为函数 $f(x)$ 在区间 $[a,b]$ 上的反常积分,记作
$\int_a^b f(x) dx$,即
$$\int_a^b f(x) dx = \lim\limits_{t \to a^+} \int_t^b f(x) dx$$
这时也称反常积分 $\int_a^b f(x) dx$ 收敛。如果上述极限不存在,则称反常积分 $\int_a^b f(x) dx$ 发散。
(2) 设函数 $f(x)$ 在 $[a,b]$ 上连续,点 $b$ 为函数 $f(x)$ 的瑕点。则可类似的定义函数 $f(x)$ 在区间 $[a,b]$ 上的反常积分
$$\int_a^b f(x) dx = \lim\limits_{t \to b^-} \int_a^t f(x) dx$$
(3) 设函数 $f(x)$ 在 $[a,b]$ 上除点 $c(a < c < b)$ 外连续,点 $c$ 为函数 $f(x)$ 的瑕点。如果反常积分
$$\int_a^c f(x) dx 和 \int_c^b f(x) dx$$
都收敛,则称反常积分 $\int_a^b f(x) dx$ 收敛,且
$$\int_a^b f(x) dx = \int_a^c f(x) dx + \int_c^b f(x) dx$$
如果 $\int_a^c f(x) dx$ 与 $\int_c^b f(x) dx$ 至少有一个发散,则称 $\int_a^b f(x) dx$ 发散。
定理 1(比较判别法)
设 $f(x), g(x)$ 在 $[a,b]$ 上连续,且 $0 \leq f(x) \leq g(x)$,$x = a$ 为 $f(x)$ 和 $g(x)$ 的瑕点,则
(1) 当 $\int_a^b g(x) dx$ 收敛时,$\int_a^b f(x) dx$ 收敛。
(2) 当 $\int_a^b f(x) dx$ 发散时,$\int_a^b g(x) dx$ 发散。
定理 2(比较判别法的极限形式)
设 $f(x), g(x)$ 在 $[a,b]$ 上非负连续,且 $\lim\limits_{x \to a^+} \frac{f(x)}{g(x)} = \lambda$(有限或无穷),则
(1) 当 $\lambda \neq 0$ 时,$\int_a^b f(x) dx$ 与 $\int_a^b g(x) dx$ 同敛散。
(2) 当 $\lambda = 0$ 时,若 $\int_a^b g(x) dx$ 收敛,则 $\int_a^b f(x) dx$ 也收敛。
(3) 当 $\lambda = +\infty$ 时,若 $\int_a^b g(x) dx$ 发散,则 $\int_a^b f(x) dx$ 也发散。
常用结论:
$$
\int_a^b \frac{1}{(x-a)^p} dx
\begin{cases}
p<1, \text{收敛}\\
p\geq 1, \text{发散}
\end{cases}
$$
$$
\int_a^b \frac{1}{(b-x)^p}dx
\begin{cases}
p<1, \text{收敛}\\
p\geq 1, \text{发散}
\end{cases}
$$
6.3 反常积分敛散性判断

七、微分方程
微分方程:含有未知函数的导数或微分的方程称为微分方程,简称方程。
微分方程的阶:微分方程中所出现的未知函数最高阶导数的阶数,称为微分方程的阶。
微分方程的解:满足微分方程的函数,称为该方程的解。
微分方程的通解:如果微分方程的解中含有任意常数,且任意常数的个数与微分方程的阶数相同,则称之为微分方程的通解。
微分方程的特解:微分方程的不含任意常数的解,称之为特解。
初始条件:确定特解的一组常数称为初始条件。
积分曲线:方程的一个解在平面上对应一条曲线,称为该微分方程的积分曲线。
7.1 一阶微分方程
7.1.1 可分离变量的方程
能表示为 $g(y)dy = f(x)dx$ 的方程,称为可分离变量的方程。求解的方法是两端积分$$ \int g(y)dy = \int f(x)dx$$
7.1.2 齐次微分方程
可化为$\frac{dy}{dx} = \varphi \left( \frac{y}{x} \right)$的微分方程称为齐次微分方程。
求解齐次微分方程的一般方法:令 $u = \frac{y}{x}$,则 $y’ = u + xu’$,从而将原方程化为 $xu’ = \varphi (u) - u$,此方程为可分离变量的方程。
求微分方程 $x^2 y’ + xy = y^2$ 满足初始条件 $y(1) = 1$ 的特解
原方程为齐次方程,可改写为 $y’ = \left( \frac{y}{x} \right)^2 - \frac{y}{x}$。令 $u = \frac{y}{x}$,则 $xu’ + u = u^2 - u$,分离变量得 $$\frac{1}{2} \left( \ln |u-2| - \ln |u|\right) = \ln |x| + C_1$$,
即$$ \frac{u-2}{u} = C x^2$$,
$$ \frac{y-2x}{y} = C x^2$$
由 $y(1) = 1$,得 $C = -1$,得所求的特解为 $\frac{y-2x}{y} = -x^2$,即 $y = \frac{2x}{1+x^2}$。
7.1.3 一阶线性微分方程
形如 $y’ + p(x)y = q(x)$ 的方程称为一阶线性微分方程。
求解一阶线性微分方程的一般方法:常数变易法,或直接利用以下通解公式 $$y = e^{-\int p(x)dx} \left[ \int q(x)e^{\int p(x)dx} dx + C \right]$$
微分方程 $(y + x^2 e^{-x})dx - xdy = 0$ 的通解是______。
解: $$(y + x^2 e^{-x}) - x \frac{dy}{dx} = 0, \quad \frac{dy}{dx} = \frac{y + x^2 e^{-x}}{x}$$
$$\frac{dy}{dx} - \frac{1}{x}y = xe^{-x}, \quad \frac{dy}{dx} - \frac{1}{x}y = xe^{-x}$$
由线性方程通解公式得
$$
\begin{align*}
y &= e^{-\int -\frac{1}{x}dx} \left( \int xe^{-x} e^{\int -\frac{1}{x}dx} dx + C \right)\\
&= x \left( \int e^{-x} dx + C \right)\\
&= x(-e^{-x} + C) = x(C - e^{-x})
\end{align*}
$$
其中C为任意常数.
7.2 可降阶的高阶方程
$y^{(n)} = f(x)$ 型的微分方程
$y’’ = f(x, y’)$ 型的方程:只需令 $y’ = p$, $y’’ = p’$,可将原方程化为一阶微分方程。
$y’’ = f(y, y’)$ 型的方程:只需令 $y’ = p$, $y’’ = p \frac{dp}{dy}$,可将原方程化为一阶微分方程。
微分方程 $yy’’ + y’^2 = 0$ 满足初始 条件$y \vert_{x=0} = 1,y’ \vert_{x=0} = 0 $的特解是______。
令 $y’ = p$,则 $y’’ = \frac{dp}{dy} p$,代入原方程得
$$
\begin{gather*}
yp\frac{dp}{dy} + p^2 = 0, \\[8pt]
y\frac{dp}{dy} = -p, \\[8pt]
\int \frac{dp}{p} = - \int \frac{dy}{y}, \\[8pt]
\ln |p| = -\ln |y| + C_1, \\[8pt]
\ln |yp| = C_1, \\[8pt]
yp = \pm e^{C_1} = C, \\[10pt]
\text{由 } y \vert_{x=0} = 1, , y’ \vert_{x=0} = \frac{1}{2} \text{ 知,} C = \frac{1}{2}, \\[8pt]
\text{则 } y \frac{dy}{dx} = \frac{1}{2}, \\[8pt]
\int y dy = \frac{1}{2} \int dx, \\[8pt]
\frac{1}{2} y^2 = \frac{1}{2} x + C_2, \\[10pt]
\text{由 } y \vert_{x=0} = 1 \text{ 知,} C_2 = \frac{1}{2}, , \text{则 } y^2 = x + 1, , y = \pm \sqrt{x+1}, \\[8pt]
\text{由 } y \vert_{x=0} = 1 \text{ 知,} y = \sqrt{x+1}.
\end{gather*}
$$
7.3 高阶线性微分方程
7.3.1 线性微分方程的解的结构
这里只讨论二阶线性微分方程,其结论可以推广到更高阶的方程。二阶线性微分方程的一般形式为
$$ y’’ + p(x)y’ + q(x)y = f(x), $$
这里的 $p(x), q(x), f(x)$ 均为连续函数。当方程右端的 $f(x) \equiv 0$ 时,称为二阶线性齐次方程,否则称为二阶线性非齐次方程。
齐次方程
$$ y’’ + p(x)y’ + q(x)y = 0 \tag{①}$$非齐次方程
$$ y’’ + p(x)y’ + q(x)y = f(x). \tag{②}$$
定理 如果 $y_1(x)$ 和 $y_2(x)$ 是齐次方程①的两个线性无关的特解,那么
$$ y = C_1 y_1(x) + C_2 y_2(x) $$
就是方程①的通解。
【注】 方程①的两个解线性无关的充要条件是它们之比不为常数。
定理 如果 $y^*$ 是非齐次方程②的一个特解,$y_1(x)$ 和 $y_2(x)$ 是齐次方程①的两个线性无关的特解,则
$$ y = C_1 y_1(x) + C_2 y_2(x) + y^*(x) $$
是非齐次微分方程②的通解。
定理 如果 $y_1^*(x), y_2^*(x)$ 是非齐次方程②的两个特解,则 $y(x) = y_2^*(x) - y_1^*(x)$ 是齐次微分方程①的解。
定理 如果 $y_1^*(x), y_2^*(x)$ 分别是方程
$$ y’’ + p(x)y’ + q(x)y = f_1(x), $$
$$ y’’ + p(x)y’ + q(x)y = f_2(x) $$
的特解,则 $y_1^*(x) + y_2^*(x)$ 是方程
$$ y’’ + p(x)y’ + q(x)y = f_1(x) + f_2(x) $$
的一个特解。
7.3.2 常系数齐次线性微分方程
二阶常系数线性齐次微分方程的一般形式为
$$ y’’ + py’ + qy = 0, \tag{③}$$
其特征方程为 $r^2 + pr + q = 0$,设 $r_1, r_2$ 为该方程的两个根。
(1) 若 $r_1 \neq r_2$ 为两个不相等的实特征根,则方程③的通解为
$$ y = C_1 e^{r_1 x} + C_2 e^{r_2 x}. $$
(2) 若 $r_1 = r_2$ 为二重实特征根,则方程③的通解为
$$ y = (C_1 + C_2 x)e^{r_1 x}. $$
(3) 若 $r_1 = \alpha + i\beta, r_2 = \alpha - i\beta$ 为一对共轭复根,则方程③的通解为
$$ y = e^{\alpha x} (C_1 \cos \beta x + C_2 \sin \beta x). $$
7.3.3 常系数非齐次线性微分方程
二阶常系数线性非齐次微分方程的一般形式为
$$ y’’ + py’ + qy = f(x). \tag{④}$$
(1) 若 $f(x) = P_m(x)e^{\lambda x}$,其中 $P_m(x)$ 为 $x$ 的 $m$ 次多项式,则方程 ④ 的特解可设为
$$ y^* = x^k Q_m(x)e^{\lambda x}, $$
其中 $Q_m(x)$ 是与 $P_m(x)$ 同次的多项式,$k$ 是特征方程含根 $\lambda$ 的重复次数。
(2) 若 $f(x) = e^{\alpha x} [P_l^{(1)}(x)\cos\beta x + P_n^{(2)}(x)\sin\beta x]$,其中 $P_l^{(1)}(x), P_n^{(2)}(x)$ 分别为 $x$ 的 $l$ 次、$n$ 次多项式,则方程 ④ 的特解可设为
$$ y^* = x^k e^{\alpha x} [R_m^{(1)}(x)\cos\beta x + R_m^{(2)}(x)\sin\beta x], $$
其中 $R_m^{(1)}(x), R_m^{(2)}(x)$ 是两个 $m$ 次多项式,$m = \max(l, n)$。
当 $\alpha + i\beta$ 不是方程 ③ 的特征根时,取 $k = 0$。
当 $\alpha + i\beta$ 是程 ③ 的单特征根时,取 $k = 1$。