线代一轮复习

​

1、行列式

---

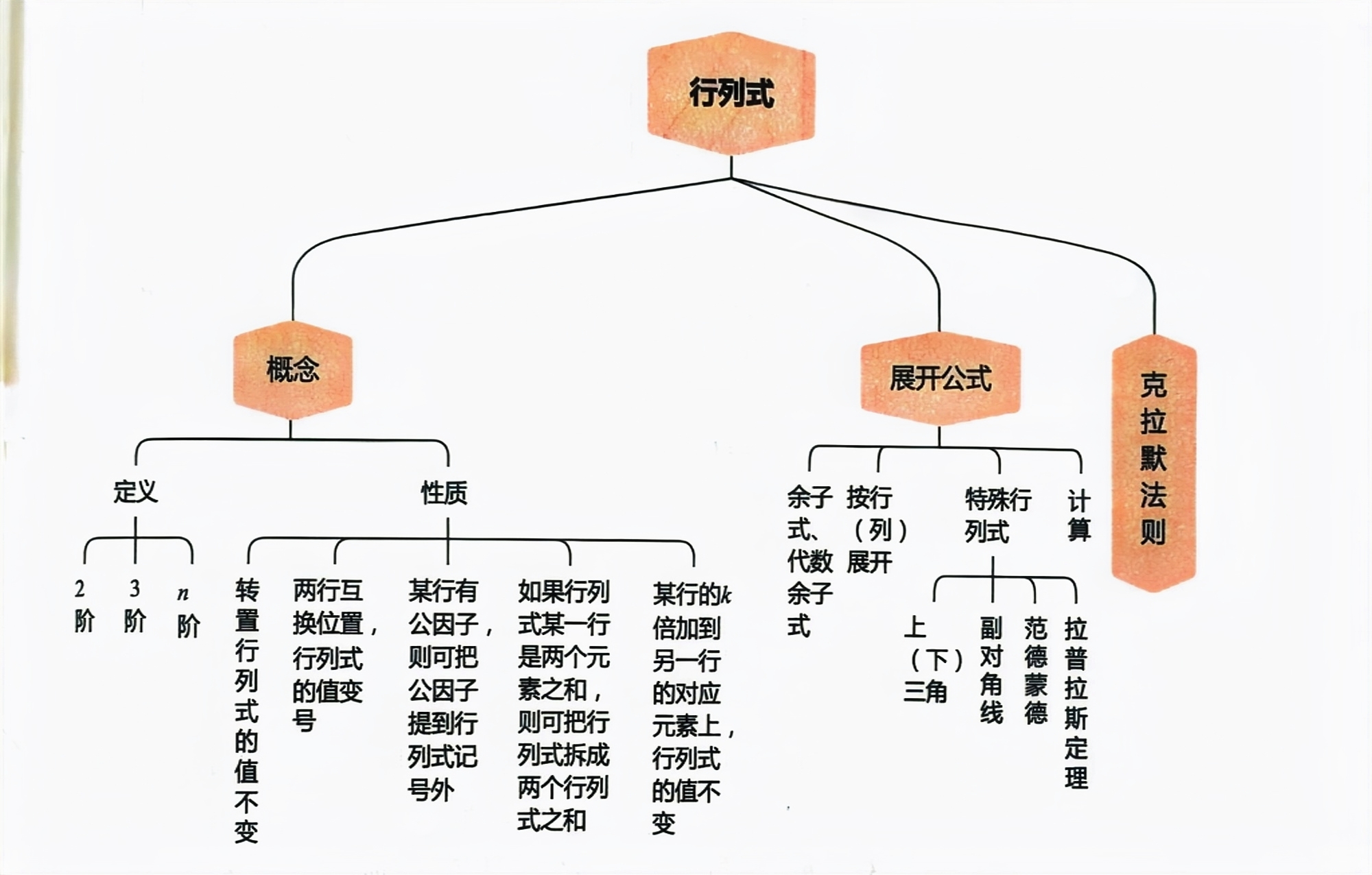
1.1 性质

1. 转置性质
   行列式转置后值不变：
   $$|A^T| = |A|$$

2. 行/列互换
   两行（或列）互换，行列式变号。若两行（或列）相同，行列式为0。

3. 公因子提取
   某行（或列）有公因子$k$，可提出：

   • 推论1：某行（或列）全为0，行列式为0。
   • 推论2：两行（或列）成比例，行列式为0。

4. 行列式拆分
   若某行（或列）为两元素之和，可拆分为两个行列式之和：
   $$
   \begin{vmatrix}a_1+b_1 & \cdots \\ \vdots & \ddots\end{vmatrix} = \begin{vmatrix}a_1 & \cdots \\ \vdots & \ddots\end{vmatrix} + \begin{vmatrix}b_1 & \cdots \\ \vdots & \ddots\end{vmatrix}
   $$

5. 倍加性质
   某行（或列）的$k$倍加到另一行（或列），行列式值不变。

1.2 行列式展开公式

1. 余子式与代数余子式

   • 余子式$M_{ij}$：划去$a_{ij}$所在行、列得到的$(n-1)$阶行列式。
   • 代数余子式$A_{ij} = (-1)^{i+j}M_{ij}$。

2. 展开定理

   • 定理1.1：行列式可按任意行（列）展开：
     $$
     |A| = \sum_{k=1}^n a_{ik}A_{ik} \quad \text{（按第$i$行展开）}
     $$

     $$
     |A| = \sum_{k=1}^n a_{kj}A_{kj} \quad \text{（按第$j$列展开）}
     $$

   • 定理1.2：不同行（列）的代数余子式乘积和为0：
     $$
     \sum_{k=1}^n a_{ik}A_{jk} = 0 \quad (i \ne j)
     $$

1.3 特殊行列式

1. 三角形行列式
   上（下）三角行列式等于主对角线元素乘积：
   $$
   \begin{vmatrix}a_{11} & \cdots & a_{1n} \\ & \ddots & \vdots \\ 0 & & a_{nn}\end{vmatrix} = a_{11}a_{22}\cdots a_{nn}
   $$

2. 副对角线行列式
   $$
   \begin{vmatrix}0 & \cdots & a_{1n} \\ \vdots & \ddots & \vdots \\ a_{n1} & \cdots & 0\end{vmatrix} = (-1)^{\frac{n(n-1)}{2}} a_{1n}a_{2,n-1}\cdots a_{n1}
   $$

3. 分块行列式（拉普拉斯展开）

• 若$A$为$m$阶，$B$为$n$阶矩阵：
  $$
  \begin{vmatrix}A & * \\ O & B\end{vmatrix} = |A|\cdot|B|
  $$

  $$
  \begin{vmatrix}O & A \\ B & *\end{vmatrix} = (-1)^{mn}|A|\cdot|B|
  $$

4. 范德蒙行列式
   $$
   \begin{vmatrix}1 & \cdots & 1 \\ x_1 & \cdots & x_n \\ \vdots & \ddots & \vdots \\ x_1^{n-1} & \cdots & x_n^{n-1}\end{vmatrix} = \prod_{1 \leq j < i \leq n} (x_i - x_j)
   $$
   注：

1.4 克拉默法则

定理1.3（克拉默法则）

对于由 ( n ) 个方程、( n ) 个未知量构成的非齐次线性方程组：
$$
\begin{cases}
a_{11}x_1 + a_{12}x_2 + \cdots + a_{1n}x_n = b_1, \\
a_{21}x_1 + a_{22}x_2 + \cdots + a_{2n}x_n = b_2, \\
\vdots \\
a_{n1}x_1 + a_{n2}x_2 + \cdots + a_{nn}x_n = b_n
\end{cases}
$$
若其系数行列式 ( $|A| \neq 0 $)，则方程组有唯一解：
$$
x_i = \frac{|A_i|}{|A|}, \quad i = 1, 2, \cdots, n
$$
其中 ($ |A_i| $) 是将 $( |A| $) 的第 ($ i $) 列替换为常数项 ( $b_1, b_2, \cdots, b_n $) 所得的行列式。

注：

1. 唯一解条件：仅当 ($ |A| \neq 0 $) 时适用。
2. 特殊情况：
   • 若 ( $|A| = 0 $)，方程组可能无解或有无穷多解，但不可能有唯一解。

推论（齐次线性方程组）

对于齐次线性方程组（常数项全为0）：

• 若 ( $|A| \neq 0 $)，方程组仅有零解 ($ x_1 = x_2 = \cdots = x_n = 0 $)。
• 若 ($ |A| = 0 $)，方程组存在非零解（无穷多解）。

2、矩阵

2.1 矩阵多项式

2.2 运算法则

(1) 加法

设 $A$, $B$, $C$ 为同型矩阵，则：

• 交换律：$A + B = B + A$
• 结合律：$(A + B) + C = A + (B + C)$
• 零矩阵：$A + O = A$（$O$ 为同型零矩阵）
• 负矩阵：$A + (-A) = O$

(2) 数乘矩阵

设 $k$, $m$ 为标量，则：

• 结合性：$k(mA) = (km)A = m(kA)$
• 分配律：$(k + m)A = kA + mA$
• 线性性：$k(A + B) = kA + kB$
• 单位数乘：$1A = A$, $0A = O$

(3) 乘法

若矩阵 $A$, $B$, $C$ 满足乘法条件，则：

• 结合律：$(AB)C = A(BC)$
• 左分配律：$A(B + C) = AB + AC$
• 右分配律：$(B + C)A = BA + CA$

(4) 转置

• 和的转置：$(A + B)^T = A^T + B^T$
• 数乘转置：$(kA)^T = kA^T$
• 积的转置：$(AB)^T = B^T A^T$
• 转置的转置：$(A^T)^T = A$

---

注：矩阵乘法一般不满足交换律（即 $AB \neq BA$）。

2.3 对角矩阵的性质与运算

对角矩阵乘法

两个对角矩阵相乘结果仍为对角矩阵，且元素为对应位置相乘:
$$
\begin{bmatrix}
a_1 & 0 & 0 \\
0 & a_2 & 0 \\
0 & 0 & a_3
\end{bmatrix}
\begin{bmatrix}
b_1 & 0 & 0 \\
0 & b_2 & 0 \\
0 & 0 & b_3
\end{bmatrix} =
\begin{bmatrix}
a_1 b_1 & 0 & 0 \\
0 & a_2 b_2 & 0 \\
0 & 0 & a_3 b_3
\end{bmatrix}
$$

性质

1. 交换律
   对角矩阵乘法可交换：$\Lambda_1 \Lambda_2 = \Lambda_2 \Lambda_1$。

2. 逆矩阵
   若对角元素均非零（$a_i \neq 0$），其逆矩阵为元素取倒数：

$$
\begin{bmatrix}
a_1 & 0 & 0 \\
0 & a_2 & 0 \\
0 & 0 & a_3
\end{bmatrix}^{-1} = \begin{bmatrix}
\frac{1}{a_1} & 0 & 0 \\
0 & \frac{1}{a_2} & 0 \\
0 & 0 & \frac{1}{a_3}
\end{bmatrix}
$$

---

2.4 伴随矩阵

设 $A$ 是一个 $n$ 阶方阵（$n \geq 2$），其伴随矩阵 $A^*$（或记作 $\text{adj}(A)$）定义为：
$$
A^* = \begin{bmatrix}
A_{11} & A_{21} & \cdots & A_{n1} \\
A_{12} & A_{22} & \cdots & A_{n2} \\
\vdots & \vdots & \ddots & \vdots \\
A_{1n} & A_{2n} & \cdots & A_{nn}
\end{bmatrix}
$$
其中 $A_{ij}$ 是矩阵 $A$ 的元素 $a_{ij}$ 的代数余子式（Cofactor），即：
$$
A_{ij} = (-1)^{i+j} M_{ij},
$$
$M_{ij}$ 是 $A$ 删去第 $i$ 行第 $j$ 列后得到的 $(n-1)$ 阶子矩阵的行列式。

---

伴随矩阵的公式：

$AA^* = A^*A = |A|E$

$(A^*)^{-1} = (A^{-1})^* = \frac{1}{|A|}A$ ($|A|\neq 0$)

$(kA)^* = k^{n-1}A^*$

$(A^*)^{\top} = (A^{\top})^*$

$|A^*| = |A|^{n-1}$

$(A^*)^* = |A|^{n-2}A$ ($n \geq 2$)

---

2.4 可逆矩阵的概念与定理

定义 设 $A$ 是 $n$ 阶矩阵，如果存在 $n$ 阶矩阵 $B$ 使得

$AB = BA = E$（单位矩阵）

成立，则称 $A$ 是可逆矩阵或非奇异矩阵，$B$ 是 $A$ 的逆矩阵，记成 $A^{-1} = B$。

定理 2.1 若 $A$ 可逆，则 $A$ 的逆矩阵唯一。

定理 2.2 $A$ 可逆 $\Leftrightarrow$ $|A| \neq 0$。

定理 2.3 设 $A$ 和 $B$ 是 $n$ 阶矩阵且 $AB = E$，则 $BA = E$。

---

3. $n$ 阶矩阵 $A$ 可逆的充分必要条件

1. 存在 $n$ 阶矩阵 $B$，使 $AB = E$（或 $BA = E$）
2. $|A| \neq 0$，或秩 $r(A) = n$，或 $A$ 的列（行）向量线性无关
3. 齐次方程组 $Ax = 0$ 只有零解
4. $\forall b$，非齐次线性方程组 $Ax = b$ 总有唯一解
5. 矩阵 $A$ 的特征值全不为 0

---

4. 逆矩阵的运算性质

若 $k \neq 0$, $A$ 可逆，则 $(kA)^{-1} = \frac{1}{k}A^{-1}$。

若 $A, B$ 可逆，则 $(AB)^{-1} = B^{-1}A^{-1}$，特别地 $(A^2)^{-1} = (A^{-1})^2$。

若 $A^{\top}$ 可逆，则 $(A^{\top})^{-1} = (A^{-1})^{\top}$；$(A^{-1})^{-1} = A$；$|A^{-1}| = \frac{1}{|A|}$。

注意 即使 $A, B$ 和 $A + B$ 都可逆，一般地 $(A + B)^{-1} \neq A^{-1} + B^{-1}$。

---

5. 求逆矩阵的方法

方法一 用公式，若 $|A|\neq0$，则 $A^{-1}=\frac{1}{|A|}A^*$。

方法二 初等变换法。$(A:E) \xrightarrow{\text{初等行变换}} (E:A^{-1})$。

方法三 用定义求 $B$，使 $AB=E$ 或 $BA=E$，则 $A$ 可逆，且 $A^{-1}=B$。

方法四 用分块矩阵。

设 $B,C$ 都是可逆矩阵，则
$$
\begin{bmatrix}
B & O \\
O & C
\end{bmatrix}^{-1} =
\begin{bmatrix}
B^{-1} & O \\
O & C^{-1}
\end{bmatrix},
\begin{bmatrix}
O & B \\
C & O
\end{bmatrix}^{-1} =
\begin{bmatrix}
O & C^{-1} \\
B^{-1} & O
\end{bmatrix}
$$

---

3、向量

3.1线性组合和线性表示

1. 给定向量组 $A：a_1,a_2,a_3,…,a_m$，对于任何一组实数$k_1,k_2,k_3,…,k_m$，表达式 $k_1a_1+k_2a_2+k_3a_3+···+k_ma_m$ 称为向量组 A 的一个线性组合，$k_1,k_2,k_3,…,K_m$称为这个线性组合的系数
2. 给定向量组 $A：a_1,a_2,a_3,…,a_m$，向量 $b$ ，如果存在一组数$λ_1,λ_2,λ_3,···,λ_m$，使 $b=λ_1a_1+λ_2a_2+λ_3a_3+···+λ_ma_m$ ，则向量 b 是向量组 A 的线性组合，这时称向量 b 能由向量组 A 线性表示

定理：

• 向量 $b$ 由向量组 $A：a_1,a_2,a_3,…,a_m$ 表示的充分必要条件是矩阵 $A=(a_1,a_2,a_3,···,a_m)$ 的秩等于矩阵 $B=(a_1,a_2,a_3,…,a_m,b)$ 的秩
• 若 A ，B能互相表示，则称他们是等价的
• 向量组 A 能由向量组 B 线性表示的充分必要条件为 $R(A)=R(A,B)$，或者$R(A) ≤ R(B)$，等价的充要条件为 $R(A)=R(B)=R(A,B)$

3.2 线性相关与线性无关

1. 给定向量组 $A：a_1,a_2,a_3,…,a_m$，存在不全为零实数$k_1,k_2,k_3,…,k_m$，使 $k_1a_1+k_2a_2+k_3a_3+···+k_ma_m = 0$ ，则称向量组 A 是线性相关的，否则称他线性无关

简单来说：

1. 线性相关：有非零解
2. 线性无关：只有零解

重要结论：

• 1. 方阵形式：直接判断行列式的值是否为零，线性相关D为0，线性无关D不为0
  2. 行数大于列数的矩阵：判断齐次线性方程组的解，线性相关有非零解，线性无关只有零解
  3. 列数大于行数的矩阵：向量个数大于维数，一定线性相关

• 向量组 $a_1,a_2,a_3,…,a_m$ 线性相关的充分必要条件是：其中至少有一个向量可由其余 m -1 个向量线性表示

• 向量组 $a_1,a_2,a_3,…,a_m$ 线性无关的充分必要条件是：其中每一个向量都不能由其余 m -1 个向量线性表示

• 若向量组 $a_1,a_2,a_3,…,a_m$ 线性无关，而向量组 $a_1,a_2,a_3,…,a_m,b$ 线性相关，则 b 可由 $a_1,a_2,a_3,…,a_m$ 线性表示，且表达式唯一

注：线性表示和线性相关性是不同的概念

---

• 若部分线性相关，则整个向量组也线性相关
• 若整体线性无关，则任意一个部分也线性无关
• 如果n维向量组$a_1,a_2,a_3,…,a_m$ 线性无关，则在每一个向量上都添加 m 个分量，得到的 n+m 维接长的向量组也线性无关
• 如果n维向量组 $a_1,a_2,a_3,…,a_m$ 线性相关，则在每一个向量上都减去 m 个分量，得到的 n-m 维截断的向量组也线性相关

---

• 向量组线性无关 ⇔ 秩等于向量个数
• 线性相关 ⇔ 秩小于向量个数

---

3.3 向量组的秩

定义：向量组的极大无关组所包含向量的个数，称为向量组的的秩

定理：

• 如果两个向量组的秩相等，且其中一个向量组可由另一个线性表示，则两个向量组等价

行向量组与列向量组：

• 行向量组的秩为行秩，列向量组的秩为列秩
• 行秩=列秩=矩阵的秩

3.4 极大无关组

定义：设向量组 $A：a_1,a_2,a_3,…,a_m$中有一部分向量组 $a_1,a_2,a_3,…,a_r (r<n)$满足

1. $a_1,a_2,a_3,…,a_r $线性无关
2. 向量组 A 中任意 $r+1$(如果有 $r+1$个向量的话) ，则称 $a_1,a_2,a_3,…,a_r $是向量组 A 的一个极大线性无关组。简称为极大无关组

  求向量组极大无关组的方法：先将列向量组构成矩阵A，然后对A实行初等行变换，把A化为行最简型矩阵，由行最简型矩阵列之间的关系，确定原向量组间的线性关系，从而确定极大无关组。(行最简型矩阵中每行首个非零元素所在的列)

---

4、线性方程组

4.1 非齐次

• 线性方程组 $A_{mn}$ * $x$=b 有解的 充要条件 是 r(A，b)= r(A)
• 当线性方程组 $A_{mn} * x$=b 有解时：r 为秩，n为系数项数，即未知量的个数(列向量个数)
  • 若 r(A，b)= r(A)=r = n，方程组有唯一解
  • 若 r(A，b)= r(A)=r < n，方 程组有无穷多解
• 同理， $A_{mn }* x $=b 无解的充要条件是 r(A，b)!=r(A)

---

4.2 齐次线性方程组解的判定

齐次线性方程组一定满足：$r(A,b)$=$r(A)$

• 齐次线性方程组$A_{mn} * x=0$ 只有零解的充要条件是 r(A)= n
• 齐次线性方程组$A_{mn} * x=0$ 有非零解的充要条件是 r(A)< n（有非零解即为无穷多解）

---

4.3齐次线性方程组的解的结构

解向量的概念

  若齐次线性方程组有非零解，则它会有无穷多解，这些解组成一个n维向量组，若能求出这个向量组的一个极大无关组，则就能用它来表示它的全部解，这个极大无关组称为齐次线性方程组的基础解系

齐次线性方程组有非零解，则它一定有基础解系。

• 定理1：如果齐次线性方程组$A_{mn} * x=0$ 的系数矩阵A的秩 $r(A)= r < n$，则$A_{mn} * x=0$ 的基础解系中有 $n-r$ 个解向量

---

4.4非齐次线性方程组的解的结构

非齐次线性方程组的解的结构为：非齐次线性方程组的特解 + 齐次线性方程组的通解。

求线性方程组通解的一般步骤

齐次线性方程组：

1. 对于增广矩阵化简为 行最简型矩阵
2. 判断解的情况并且得到解向量的个数 = n-r
3. 通过行最简矩阵得到自由未知量，首非零元与自由未知量确定方程，求方程解，得到各个未知量的解，并且得到每一个基础解系
4. 通解为 各个基础解系的k倍和

非齐次线性方程组：

1. 步骤与上面基本一致，但是通解为：特解 + 导出组（导出组指的是常数项为0）的基础解系

---

5、特征值和特征向量

---

6、二次型